by W.A. Steer PhD
![]()
by W.A. Steer PhD
| Back to contents | About... |
![]()
Digital Signal Processing (DSP) is a vast and fascinating subject which has exploded in application in recent decades. In its simplest form, high-pass, low-pass, notch, or bandpass filters can be implemented in the digital domain, with far greater precision and stabilty than analog counterparts, and very often at much lower cost. Fourier Transform techniques, impossible in the analogue domain, facilitate highly robust and spectrally-efficient modulation methods used in communications systems such as dial-up modems and digital television and radio broadcasts. State-of-the-art non-linear and data-dependent processing are at the core of all modern audio and video compression systems such as MP3 and MPEG. This page attempts to introduce the key concepts, with practical examples, from an applications, engineering and programming perspective.
A large part of Digital Signal Processing (DSP) is concerned with frequency-domain processing; this page introduces basic Fourier techniques, concepts of signals, modulation and sidebands, and will demonstrate the methods used for detection and filtering of specific-frequency signals in a dataset (such as DTMF tones in an audio file).
| y(t) = sin(wt) |
| y(t) = sin(2πft) |
| yi = sin(2π·i·f / fs) |
Real DSP program-code will usually use the final form of the wave equation in practice.
Beware that for mathematical working, indentities, and proofs, I'll stick with less cumbersome notation!
In physics and electronics we tend to use the phrase 'sine wave' to describe the waveform of a single, pure, frequency without being unduly concerned with its phase. Phase is important in maths and DSP, so we will use 'sin' and 'cos' carefully.
From the standard trigonometric identity:
| sin(A+B) = sinA·cosB + cosA·sinB |
we can justify that for a sine wave of arbitrary phase offset, Δ, relative to a reference (such as the start of our buffer):
| sin(φt+Δ) = sin(φt)·cosΔ + cos(φt)·sinΔ |
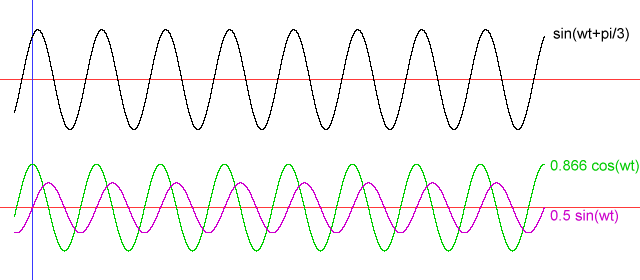
Figure 1: Example - sinewave of arbitrary phase analysed as a composite of a sine and cosine 'basis function' waves.
Introducing an arbitrary amplitude, A, for our sinewave, we can generalise this one step further:
| A·sin(φt+Δ) = I·sin(φt) + Q·cos(φt) |
The phase offset is now implicitly encoded; in this example, Δ = arctan(Q / I)
[In practical programming, avoid using tan and arctan functions as they have a nasty habit of
causing overflow or division-by-zero errors!]
The original amplitude is given by:
| A = sqrt(I2+Q2) |
The basic Fourier integral results tells us that when averaged over an integer number of cycles, the product of two sine (or cosine) terms is ½ if the frequencies are identical, and otherwise zero:
| π | { | 0 | m!=n | ||
| (1/2π)· | ∫ | sin mx ·sin nx dx = | { | ½ | m=n!=0 |
| -π | { | 0 | m=n=0 |
| π | { | 0 | m!=n | ||
| (1/2π)· | ∫ | cos mx ·cos nx dx = | { | ½ | m=n!=0 |
| -π | { | 1 | m=n=0 |
where m and n are integer.
Also note that the integral product of mixed sin and cos terms always equals zero.
| π | |||||
| (1/2π)· | ∫ | sin mx ·cos nx dx = | 0 | ||
| -π |
As we shall see later, these results are the key to being able to detect the presence (amplitude and phase) of single-frequency components in arbitrary digitised signals.
Going one step further, Fourier showed that any arbitrary periodic function f(x) (periodic in {-π,π}) can be analysed as a series of coefficients of sine and cosine harmonic terms:
| f(x) = ½·a0 + a1·cos x + b1·sin x + a2·cos 2x + b2·sin 2x + a3·cos 3x + b3·sin 3x + ... |
| π | |||||
| an = (1/π)· | ∫ | f(x) ·cos nx dx | |||
| -π |
| π | |||||
| bn = (1/π)· | ∫ | f(x) ·sin nx dx | |||
| -π |
These are absolutely fundamental results for any kind of Digital Signal Processing (DSP) involving detection or analysis of periodic frequencies in data.
Note: a harmonic frequency component in f(x) which has a phase shift such that it is offset from both the
sine and cosine analysis functions will contribute to a mixture of both the
corresponding an and bn coefficients.
The amplitude of any present component, regardless of phase, can always be calculated as
sqrt(an2 + bn2) .
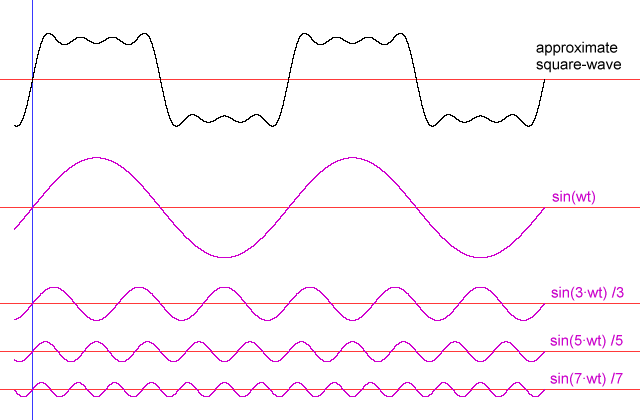
Figure 2: Example - square-wave synthesised using Fourier cosine coefficients an = 0, and
sine coefficients bn = { (1/n), n odd; 0, n even }
Note: You will often see Fourier integrals and related theory written using eiφ notation, where:
| eiφ = cos φ + i·sin φ |
This notation is very compact, and enables both the cosine and sine terms to be expressed in a single equation, but can take some getting used to. In many programming languages you'll need to revert to explicit sin() and cos() for the coding anyway. For that reason, this is the last of eiφ on this page!
| sin(φt) · { A·sin(φt+Δ) } = ½·A·{ cos(Δ) - cos(2φt+Δ) } |
| cos(φt) · { A·sin(φt+Δ) } = ½·A·{ sin(Δ) + sin(2φt+Δ) } |
and just for completeness...
sin(φt) · { A·cos(φt+Δ) } = ½·A·{ -sin(Δ) + sin(2φt+Δ) }
cos(φt) · { A·cos(φt+Δ) } = ½·A·{ cos(Δ) + cos(2φt+Δ) }
When these results are numerically summed over an integer number of cycles, the cos(2φt+Δ) and sin(2φt+Δ) terms average out to zero, leaving:
| ∑ sin(φt) · { A·sin(φt+Δ) } = ½·A· ∑ cos(Δ) = ½·A·N·cos(Δ) |
| ∑ cos(φt) · { A·sin(φt+Δ) } = ½·A· ∑ sin(Δ) = ½·A·N·sin(Δ) |
where N is the number of samples (data-points) summed over.
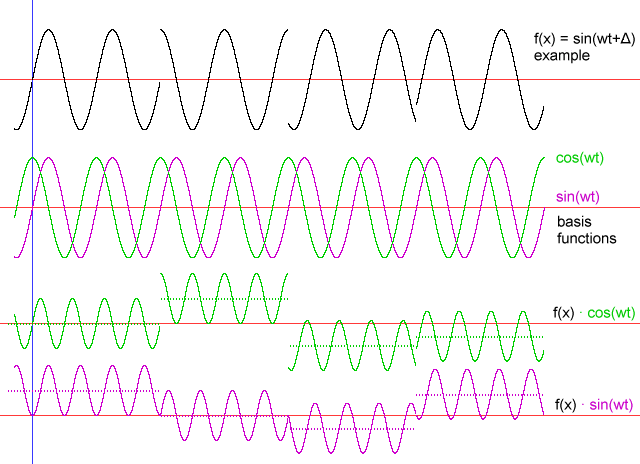
Figure 3: Example - multiplication of example waveform by sin() and cos() basis functions. The steady-state offset
is equal to half the magnitude of that component in the original signal, and can be negative.
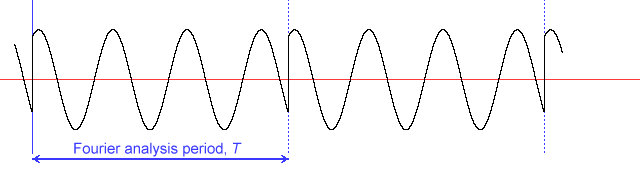
Figure 4: A signal frequency which is not periodic in the Fourier analysis period, T, is still
'perceived' by the analysis as cyclical.
A signal frequency which is not periodic in the Fourier analysis period, T, is still 'perceived' by the analysis as cyclical (refer to figure 4). Consequently the analysis typically 'sees' step disjoints in the waveform with a periodicity equal to the analysis period. These disjoints lead to a 'splatter' of rogue harmonics of the analysis period to appear in a full Fourier transform, as well as spurious responses in single-frequency analyses. Further, because we now have an incomplete number of waveform cycles, the average value in the analysis period of this example has become non-zero... we've inadvertently created an apparent DC offset!
A neat solution is to 'window' your source-data. In concept, you gracefully 'fade out' the waveform at each end of your analysis-period. This trick removes the end-effect 'glitches', and introduces a well-behaved pseudo-periodicity.
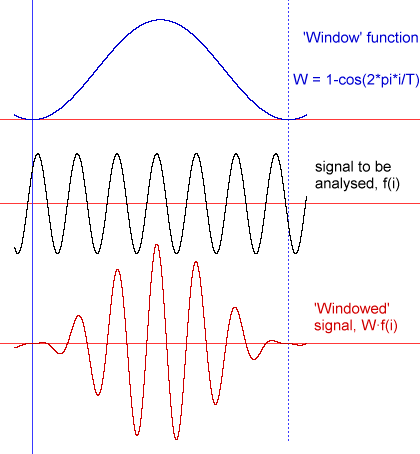
Figure 5: 'Windowing' a signal
A commonly-used windowing function is the basic 'raised cosine' window, W=1-cos(2π·i/T) [i is the sample-number, and T is the total number of samples in the window], and is a good starting-point. This window is simple and has the advantage that a time-series of windows can be 50%-overlapped with constant overall amplitude-sensitivity.
You may have observed that a single frequency source signal ( fc ), windowed with the raised cosine function, looks just like an amplitude-modulated (radio) signal, with modulation frequency fm = 1/T samples. Strictly fm = fs· 1/T Hz, where fs is the sampling frequency.
An alternative, and equally valid, intepretation of an AM signal with a fixed modulation frequency, is as a carrier of constant amplitude accompanied by two 'sidebands' with frequencies fc ± fm, each with amplitude equal to one half of the nominal carrier amplitude (if 100% modulation depth to start with).
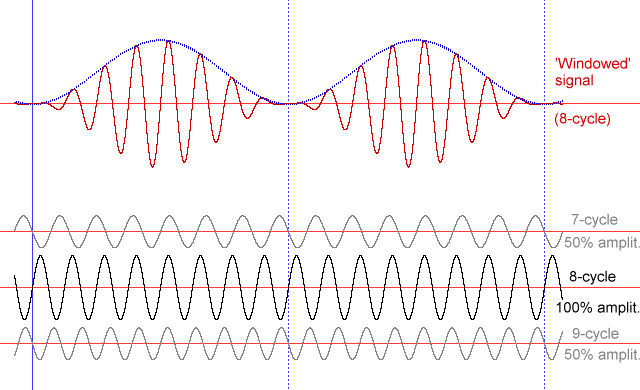
Figure 6: Example windowed-signal and its frequency components
Consequently, the raised-cosine-windowed Fourier transform of a sinewave which is periodic in the period of the transform, 'spills' half its amplitude into the two frequency-bins adjacent to that corresponding to the true frequency. This may seem like a bad thing, but the beauty is that the corresponding transform of a sinewave which is not periodic in the transform again only 'spills' relatively locally, rather than contaminating the entire spectrum.
Plenty of alternative window functions are used, with various benefits and drawbacks, and people tend to be very opinionated over which is 'best'. It all depends on the application, but different windows trade-off time- and frequency-resolution, and the exact form of the inevitable 'energy' spillage into adjacent bins (and how much it depends on the distance between the input frequency and the discrete bin-frequencies). Be aware that other windows are available!
A wide window (wide in time, or space) will have a slow response in time, but a sharp (precise) frequency response. A narrow window (narrow in time, or space) will have a faster time response, but a broader frequency response.

©2005 William Andrew Steer